上 tan(π/2-θ) 246049-Tan(pi/2-theta)

View Notes Math123_trig_reviewpdf from MATH 123 at University of Saskatchewan Math 123 1718 Trigonometry Review L Walter Angles The radian measure of aFind x from the following equation x cot(π/2 θ) tan(π/2 θ) sin θ cosec(π/2 θ) = 0 ← Prev Question Next Question → 0 votesTan (π/2θ) sin²θ cos²θ Pythagorean identity 1 1 tan²θ Pythagorean identity sec

Calculate The Value Of Tan Pi 2 Pi 6 Brainly In

Tan(pi/2-theta)

Tan(pi/2-theta)-Solution for If sin θ = 1/4 and θ is acute, find tan (π/2 θ) Social Science AnthropologyCotangent cot (or cotan or cotg or ctg or ctn) adjacent/opposite cot⁡θ=cos⁡θsin⁡θ=tan⁡(π2−θ)=1tan⁡θ{\displaystyle \cot \theta ={\frac {\cos \theta }{\sin \theta }}=\tan \left({\frac {\pi }{2}}\theta \right)={\frac {1}{\tan \theta }}}

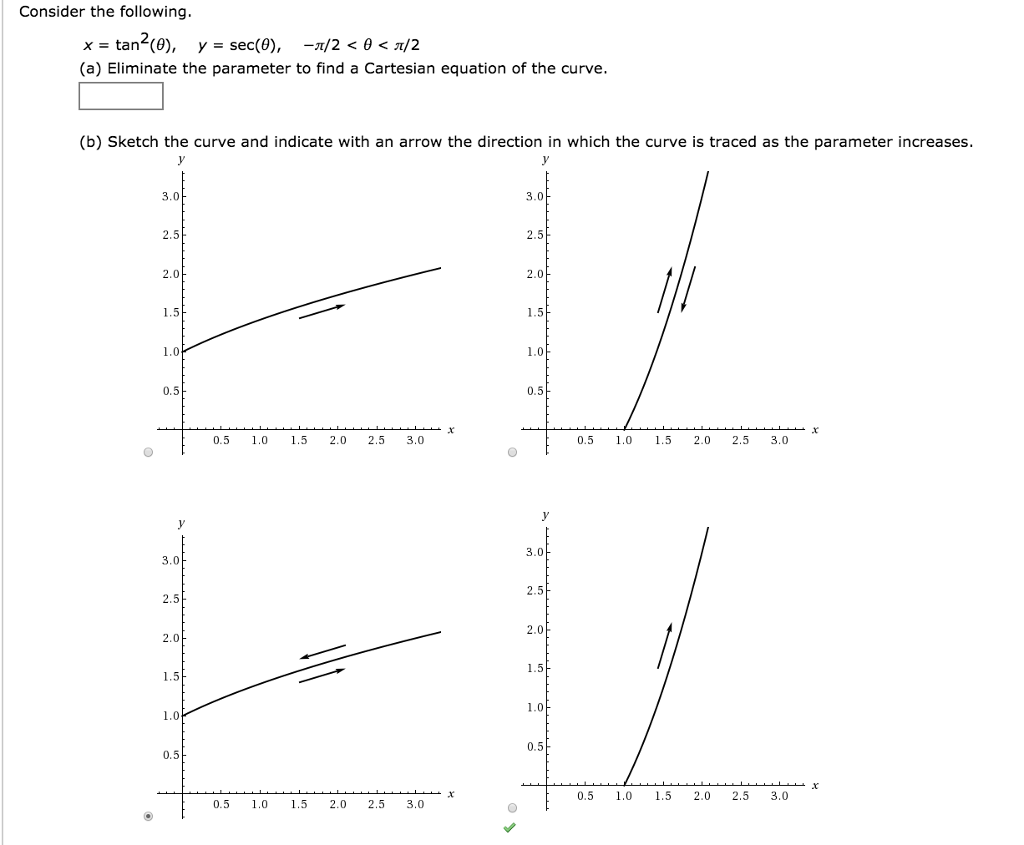
18 Find The Cartesian Equation Of The Curve From The Parametric Equations X Tan 2 Theta And Y Sec Theta Where Pi 2 Theta Pi 2 Then Sketch It Width Indication Of

Recall that the tangent function has a period of π π On the interval 0, π), 0, π), and at the angle of π 4, π 4, the tangent has a value of 1 However, the angle we want is (θ − π 2) (θ − π 2) Thus, if tan (π 4) = 1, tan (π 4) = 1, thenTan (π/2−θ)＝1/tanθの証明 のθを、−θにおきかえてみます。 ここで、" tan (−θ)＝−tanθ "の 公式 より、 ・ 三角関数の不等式sin (θ＋π/2)≧1/√2 角度の部分が複雑な不等式の計算問題 ・ y＝sin (2θπ/2)のグラフの書き方 三角関数のグラフ ・ 三角関数tanθを含む不等式の基本問題 ・ 三角関数の性質 θ＋π/2の角の公式の証明 ・ 三角関数の単位円 もっと見るGet stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!

答案解析 举报 这个要用到三角函数的定义 在α的终边取一点A（x,y) 过A做x轴垂线M,在AMO中 tana=y/x tan (π/2α)=x/y 所以tan (π/2α)=1/tana So tan( x 2) → − 3 Now cos( x 2) = 1 sec(x 2) = − 1 √1 tan2(x 2) = − 1 √1 ( − 3)2 = − 1 √10 Again sin( x 2) = tan( x 2) × cos( x 2) = − 3 ×( − 1 √10) = 3 √10 Answer linkSubstitution Theorem for Trigonometric Functions laws for evaluating limits – Typeset by FoilTEX – 2

ピタゴラスの定理 や オイラーの公式 などから以下の基本的な関係が導ける 。 cos 2 ⁡ θ sin 2 ⁡ θ = 1 {\displaystyle \cos ^ {2}\theta \sin ^ {2}\theta =1\!} ここで sin2 θ は (sin (θ))2 を意味する。 この式を変形して、以下の式が導かれる： sin ⁡ θ = ± 1 − cos 2 ⁡ θ {\displaystyle \sin \theta =\pm {\sqrt {1\cos ^ {2}\theta }}}The PDF for Chapter 3, exemplar problems and solutions can be downloaded and practised offline as well Chapter 3 of NCERT Exemplar Solutions for Class 11 Maths Trigonometric Functions explains domain and range of trigonometric functions Trigonometric Functions can simply be defined as the functions of an angleIf −π/2 < θ < π/2, then −∞ < tan(θ) < ∞, so −0 ≤ tan2(θ) < ∞, and thus 0 ≤ x Also, if −π/2 < θ < π/2, then sec(θ) ≥ 1, so the graph of the parametric equations is in the first quadrant, with yvalues always greater than or equal to one

Pplato Flap Math 3 2 Polar Representation Of Complex Numbers

If Tan Pcosx Cot Psinx Then Prove That Cos X P 4 1 2 2 Brainly In

 Given tanΘ= 5/12 and π/2Tan (theta)=2 tan (θ) = 2 tan ( θ) = 2 Take the inverse tangent of both sides of the equation to extract θ θ from inside the tangent θ = arctan(2) θ = arctan ( 2) Evaluate arctan(2) arctan ( 2) θ = θ = The tangent function is positive inThe following Key Idea outlines the procedure for each case, followed by more examples Key Idea 1 Trigonometric Substitution (a) For integrands containing √a2 x2 Let x = asinθ, for π / 2 ≤ θ ≤ π / 2 and a > 0 On this interval, cosθ ≥ 0, so √a2

Www Shsu Edu Kws006 Precalculus 4 6 Inverse Trig Functions Files S 26z 10 6 Pdf

Ex 2 1 14 Find Value Of Tan 1 Root 3 Sec 1 2 Ex 2 1

 If cot θ= 2, find the exact value of a)tanθ b)csc2θ c) tan(π/2 θ) d)sec2θ This problem has been solved! いきなり tan の加法定理を使うと tan (π/2) が出てきてしまうので、このままでは使えませんが、以下のように一度 sin、 cos が出てくる形にするとできそうです。 tan (π/2θ)=sin (π/2θ)/cos (π/2θ) = {sin (π/2)cosθcos (π/2)sinθ}/ {cos (π/2)cosθsin (π/2)sinθ} = {1・cosθ0Find maximum value of x for which 2 tan−1xcos−11−x21x2 is independent of x 0 2 3 1 Let x=tan θ−π2

Pplato Flap Math 3 2 Polar Representation Of Complex Numbers

General Solution Of Tantheta Tan Pi 2 Theta 2 Is

Solution for If θ is an acute angle and cot θ = 1/4, find tan (π/2 θ)θ＋π/2，θπの公式導き方② 次は計算をしない覚え方を紹介です。 1つ目に関数の形です。 まず\(\pi\)の整数倍が絡むものは関数の部分が変化しません。 \(\displaystyle \frac{\pi}{2}\)の奇数倍が絡むものは sin cos，\(tan \displaystyle \frac{1}{\tan}\)と変化します。Returns Double An angle, θ, measured in radians, such that π ≤ θ ≤ π, and tan(θ) = y / x, where (x, y) is a point in the Cartesian planeObserve the following For (x, y) in quadrant 1, 0 < θ < π/2For (x, y) in quadrant 2, π/2 < θ ≤ πFor (x, y) in quadrant 3, π < θ < π/2For (x, y) in quadrant 4, π/2 < θ < 0For points on the boundaries of the quadrants, the return

Solved Tan P 4 Theta 2 1 Sec Theta Tan Theta Brainly In

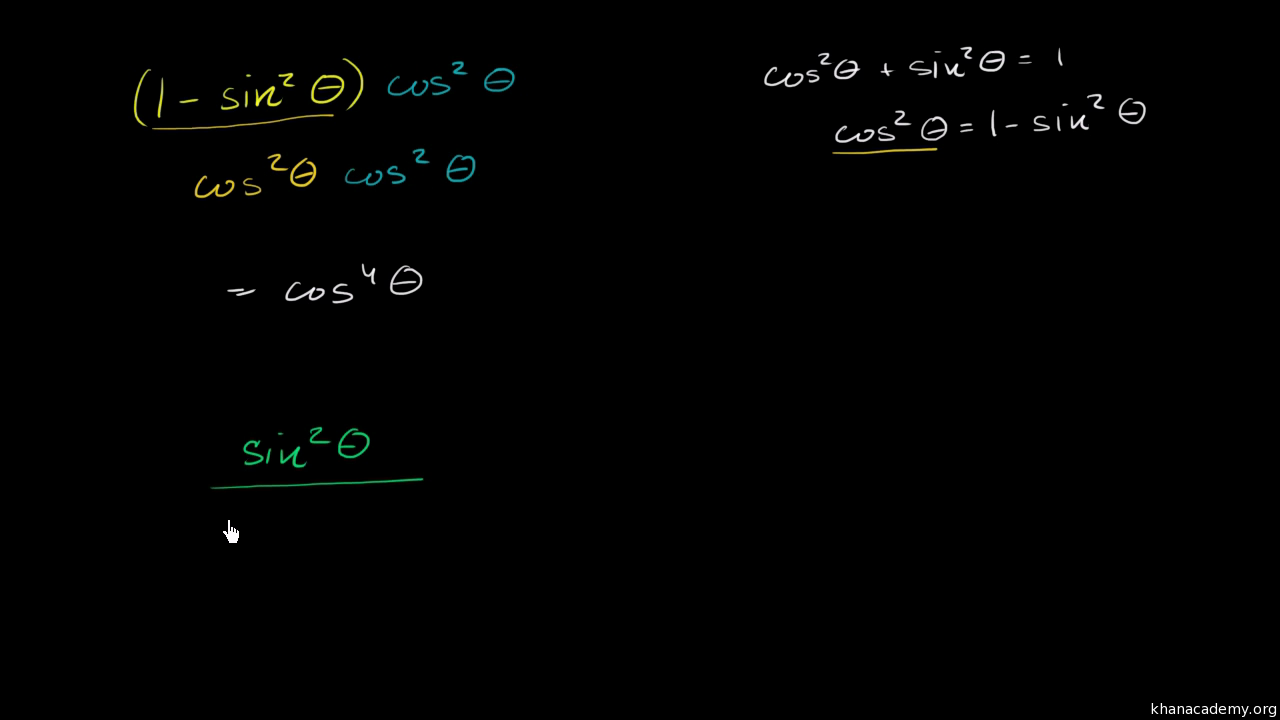
Using Trigonometric Identities Video Khan Academy

To prove the identity cot(π/2) ‒ θ = tan θ , we'll start by utilizing the following basic identity cot θ = cos θ/sin θ Therefore, substituting on the left side, we have cos(π/2 ‒ θ) ∕Given tan 5θ=cot 2θ ⇒ tan 5θ= tan(π 2−2θ) ⇒ 5θ=nπ π 2−2θ ⇒ 7θ=nπ π 2 ⇒ θ= nπ 7 π 14,n∈ ZClick here👆to get an answer to your question ️ lf x = log Tan ( π/4 θ/2) ,then cos h(x) =

Tantheta Tan Pi 3 Theta Tan 2pi 3 Theta 3

Cos Pi 2 Theta Sec Theta Tan Pi Theta Sec 2pi Theta Sin Pi Theta Cot Pi 2 Theta Maths Trigonometric Functions Meritnation Com

 i LHS = cos 2 π θ cos e c 2 π θ tan π 2 θ sec π 2 θ cos θ cot π θ = cos θ cosec θ cot θcos e c θ cos θ cot θ =cos θ cosec θ cot θCos θ = sin ( π 2 − θ) sin θ = cos ( π 2 − θ) tan θ = cot ( π 2 − θ) cot θ = tan ( π 2 − θ) sec θ = csc ( π 2 − θ) csc θ = sec ( π 2 − θ) Fundamental Identities tan θ = sin θ cos θ sec θ = 1 cos θ csc θ = 1 sin θ cot θ = 1 tan θ = cos θ sin θTan(π/2θ) ① Simplifica la expresión cot(θ)

Finding Principal Value Of Inverse Trigonometric Functions Teachoo

Sin Pi 2 Theta Cos 3pi 2 Theta Tan 5pi 2 Theta Cot 7pi 2 Theta Youtube

The formula used (i) tan θ = cot (π/2 θ) (ii) cot θ = tan (π/2 θ) We have, tan1(cot x) cot1(tan x) Now, we can see that tan1(cot x) cot1(tan x) = π 2x Now differentiating, Please log in or register to add a comment ← Prev Question Next Question → A Computer Science portal for geeks It contains well written, well thought and well explained computer science and programming articles, quizzes and practice/competitive programming/company interview Questions= tan(π / 2 θ r) (4) θ (degrees) Trigonometric functions ranging 0 to 90 degrees are tabulated below Trigonometric functions in pdfformat;

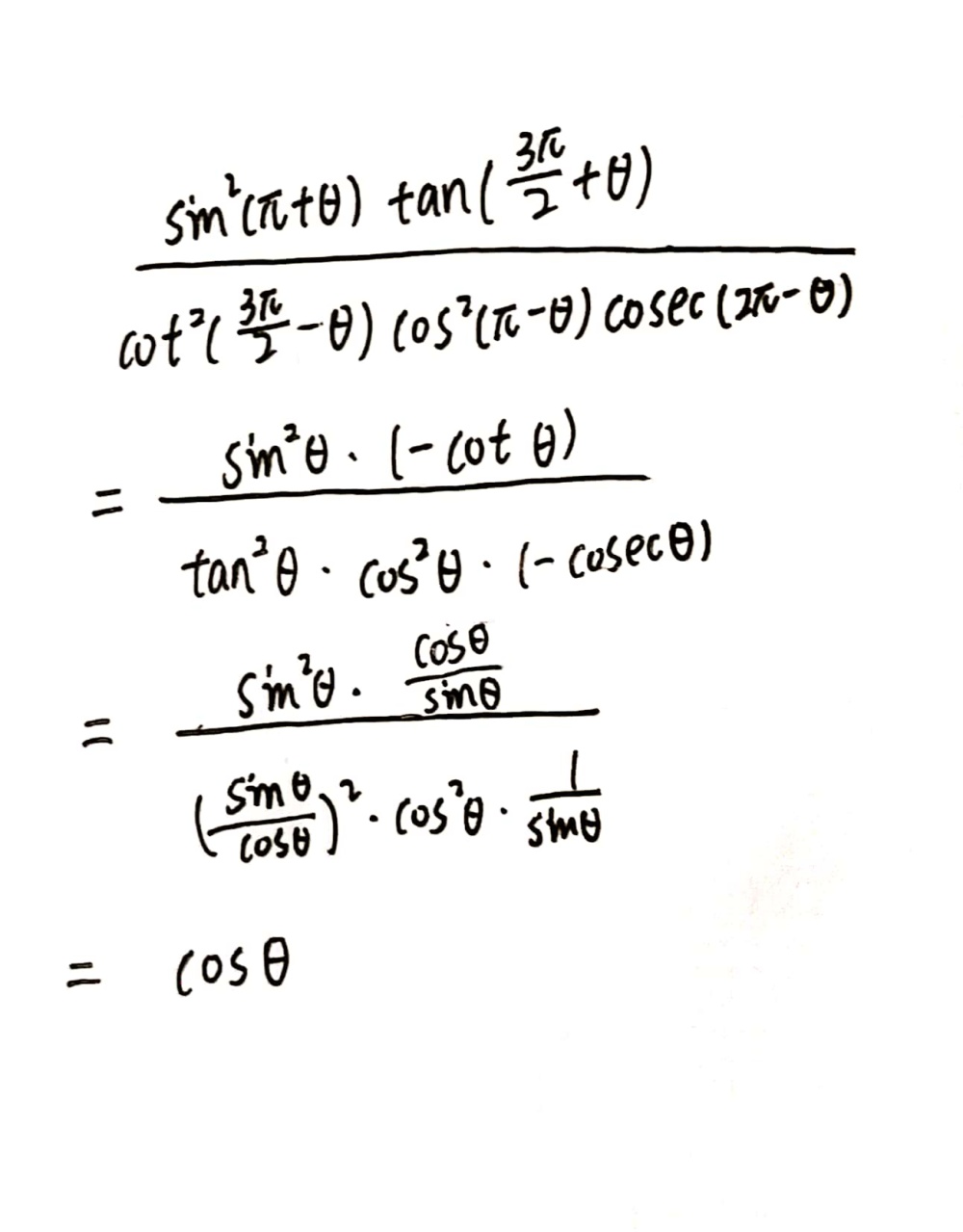
Frac Sin 2 P 8 Tan Frac 3 P 2 8 Cos 2f Gauthmath

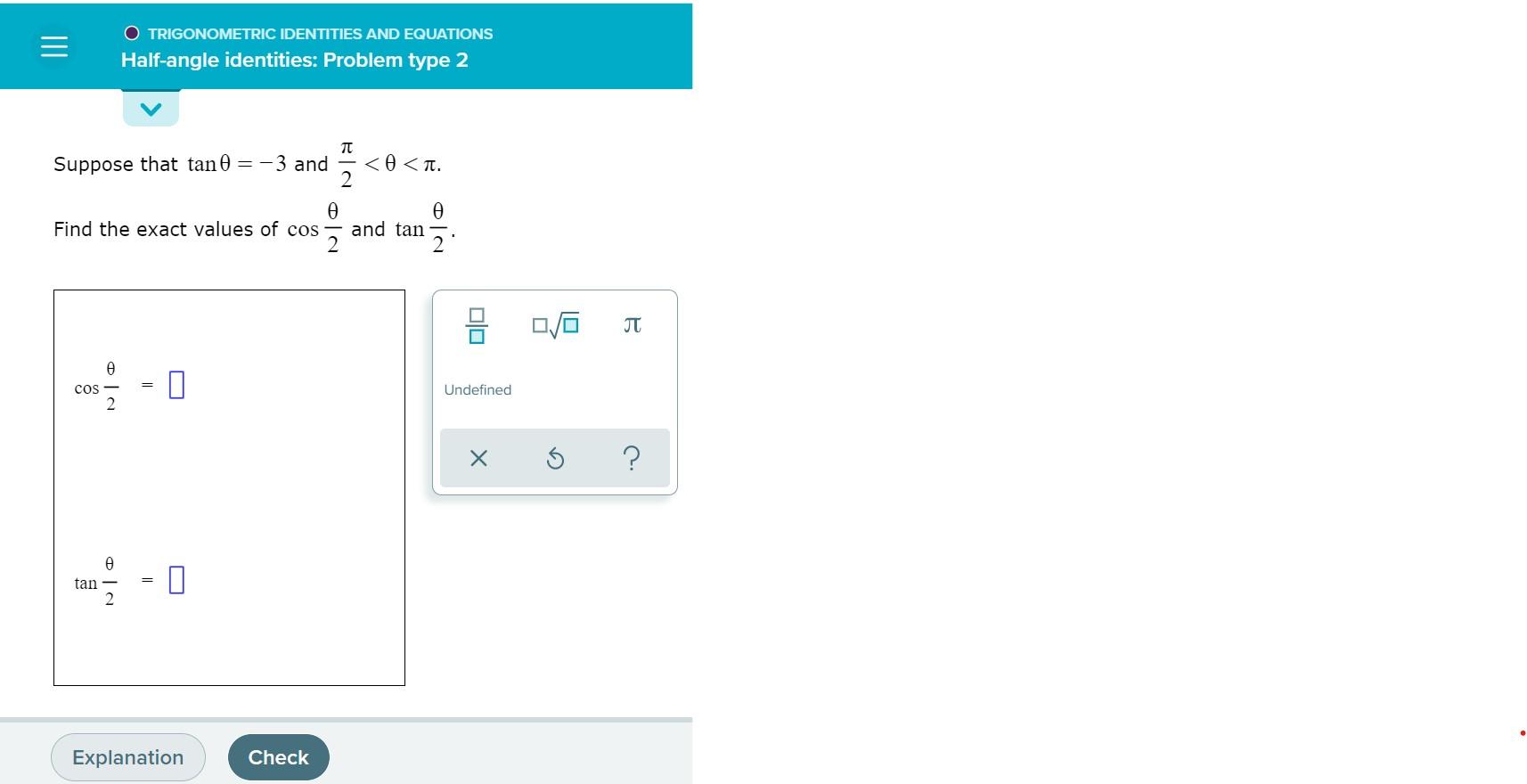
Solved 1 Suppose That Tan 3 And Pi 2 Theta Pi Fin Chegg Com

高校数学 三角関数 公式 sin（π/2θ) cos（π/2θ) tan（π/2θ)の覚え方 導き出し方D θ d ( cos ( θ) sin ( θ) ) For any two differentiable functions, the derivative of the quotient of two functions is the denominator times the derivative of the numerator minus the numerator times the derivative of the denominator, all divided by the denominator squared π 2 \dfrac {\pi} {2} 2π の奇数倍でないような任意の実数 α, β \alpha,\beta α,β に対して） tan ⁡ ( α β) = tan ⁡ α tan ⁡ β 1 − tan ⁡ α tan ⁡ β \tan (\alpha\beta)=\dfrac {\tan\alpha\tan\beta} {1\tan\alpha\tan\beta} tan(α β) = 1−tanαtanβ tanα tanβ

Prove That Sec Theta Tan Theta Tan Pi 4 Theta 2

Tinkutara Equation Editor Math Forum Question

Inverse functions arcsin (a) = sin1 (a) (1a) arccos (a) = cos1 (a) (2a) arctan (a) = tan1 (a) (3a)See the answer See the answer See the answer done loadingTan^ {1} (0) \square!

Check My Work Evaluating Tan Frac 7 Pi 8 Using A Half Angle Formula Mathematics Stack Exchange

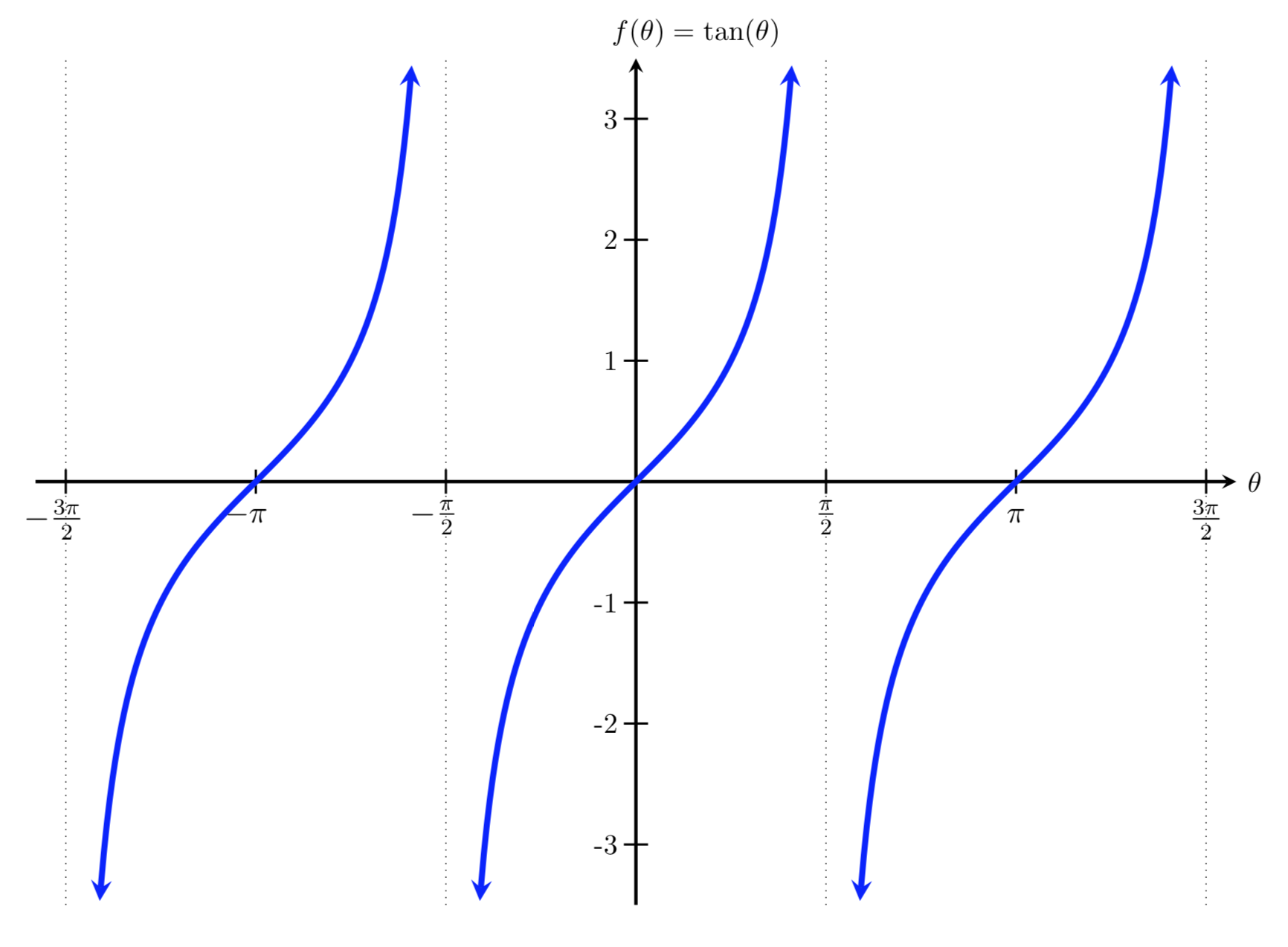
Mfg The Tangent Function And Cofunctions

You can do it in several ways Let theta = t cot A = 1/tan A cot (t pi) = 1/(tan (t pi) = 1/(tan t tan pi)/(1 tan t*tan pi tan pi = sin pi/cos pi = 0/1 = 0 So , Cot (t pi) = 1/tan t = cot t tan1 (tan θ) = θ, π/2 < θ < π/2 30 cosec1 (cosec θ) = θ, – π/2 ≤ θ < 0 or 0 < θ ≤ π/2 31 sec1 (sec θ) = θ, 0 ≤ θ ≤ π/2 or π/2< θ ≤ π 32 cot1 (cot θ) = θ, 0 < θ < π 33 \(\sin ^{1}x \sin ^{1}y=\sin ^{1}(x\sqrt{1y^{2}}y\sqrt{1x^{2}}), if x, y \geq 0 and x^{2}y^{2} \leq 1\) 34Find an answer to your question u= log tan(π/4x/2) prove that, sinh u = tan x parthjadav parthjadav Math Secondary School answered U= log tan(π/4x/2) prove that, sinh u = tan x 1 See answer parthjadav is waiting for your help Add

If Tan Pi Cos Theta Cot Pi Sin Theta Then Cos 2 Theta

Using The Identity Sin 2 8 Cos 2 8 1 Find Gauthmath

Pythagorean identities Main article Pythagorean trigonometric identity In trigonometry, the basic relationship between the sine and the cosine is given by the Pythagorean identity sin 2 ⁡ θ cos 2 ⁡ θ = 1 , {\displaystyle \sin ^ {2}\theta \cos ^ {2}\theta =1,} Cos (2 π θ)cosec(2πθ)tan(π/2θ) = 1sec(π/2θ) cosθ cot(πθ) Share with your friends Share 0We know that cot θ = tan (π/2 – θ) ∴ If tan x = tan y, then x is given by x = nπ y, where n ∈ Z From above expression, on comparison with standard equation we have y = ∴ ⇒ ⇒ ,where nϵZ ans Question 26 Find the general solutions of the following equations tan 2x tan x = 1 Answer Ideas required to solve the problem

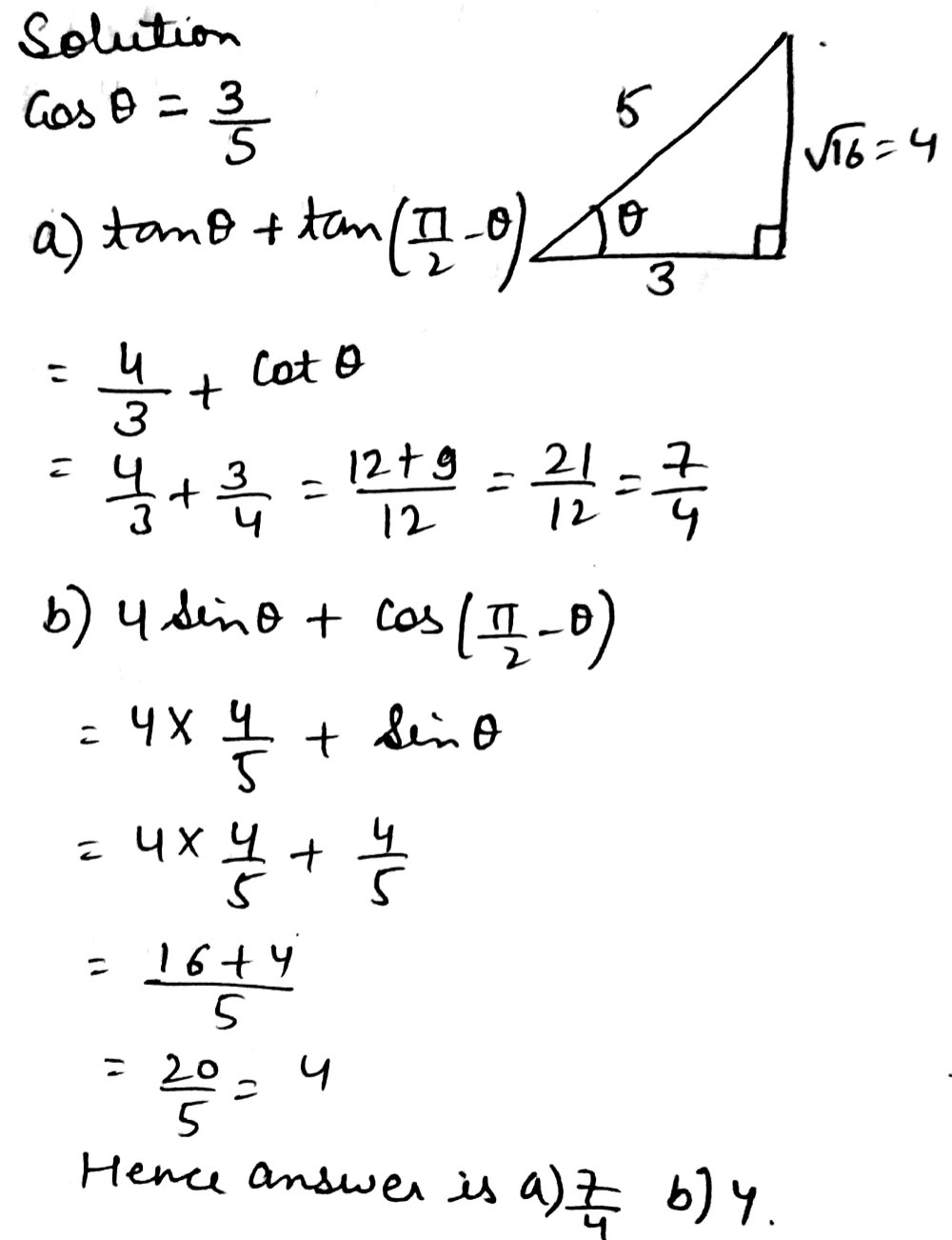
2 Given That Cos 8 3 5 Find That 8 Is Gauthmath

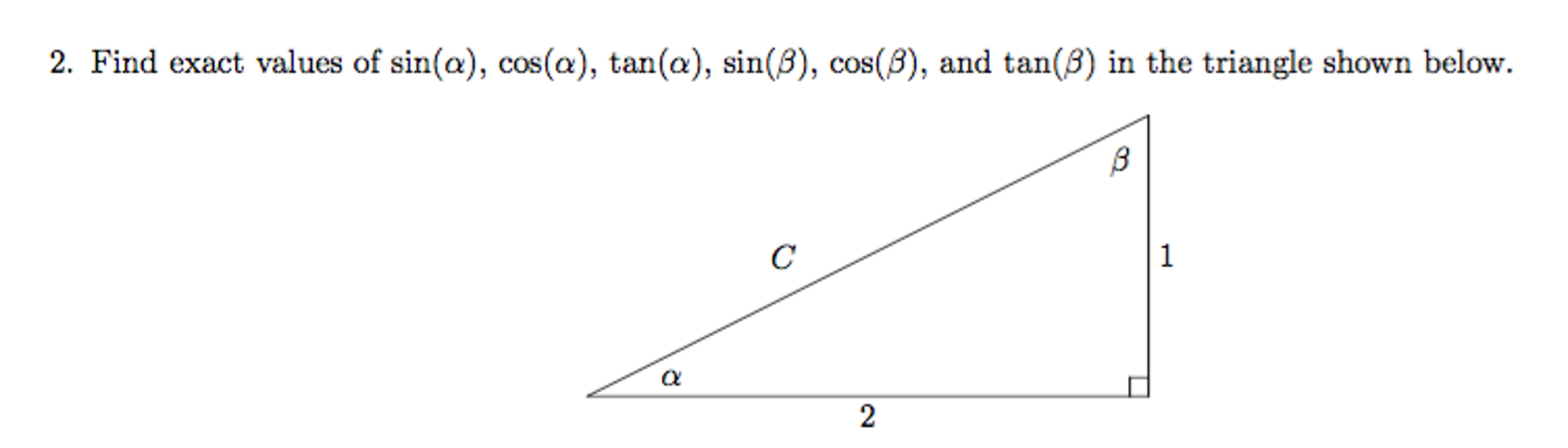
Suppose The Angle Theta Is In The Fourth Quadrant 3 Chegg Com

= t a n (4 π 2 θ ) c o t (4 π 2 θ ) 2 × (t a n (4 π 2 θ ) c o t (4 π 2 θ ) ) t a n (4 π 2 θ ) − c o t (4 π 2 θ ) multiply denominator and numerator by t a n ( 4 π 2 θ ) c o t ( 4 π 2 θ ) Expand the left side using the trigonometric identities ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯∣∣ ∣ 2 2tan( π 2 − θ) = cotθ2 2∣∣ ∣ −−−−−−−−−−−−−−−−−−−−−− and ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯∣∣ ∣ 2 2cotθ = cosθ sinθ,tanθ = sinθ cosθ 2 2 ∣∣ ∣ −−−−−−−−−−−

Chapter 5 Analytic Trigonometry 5 1 Fundamental Identities Ppt Download

These Two Methods Of Solving The Tan 2 Theta Frac Pi 4 Which One Is Correct Mathematics Stack Exchange

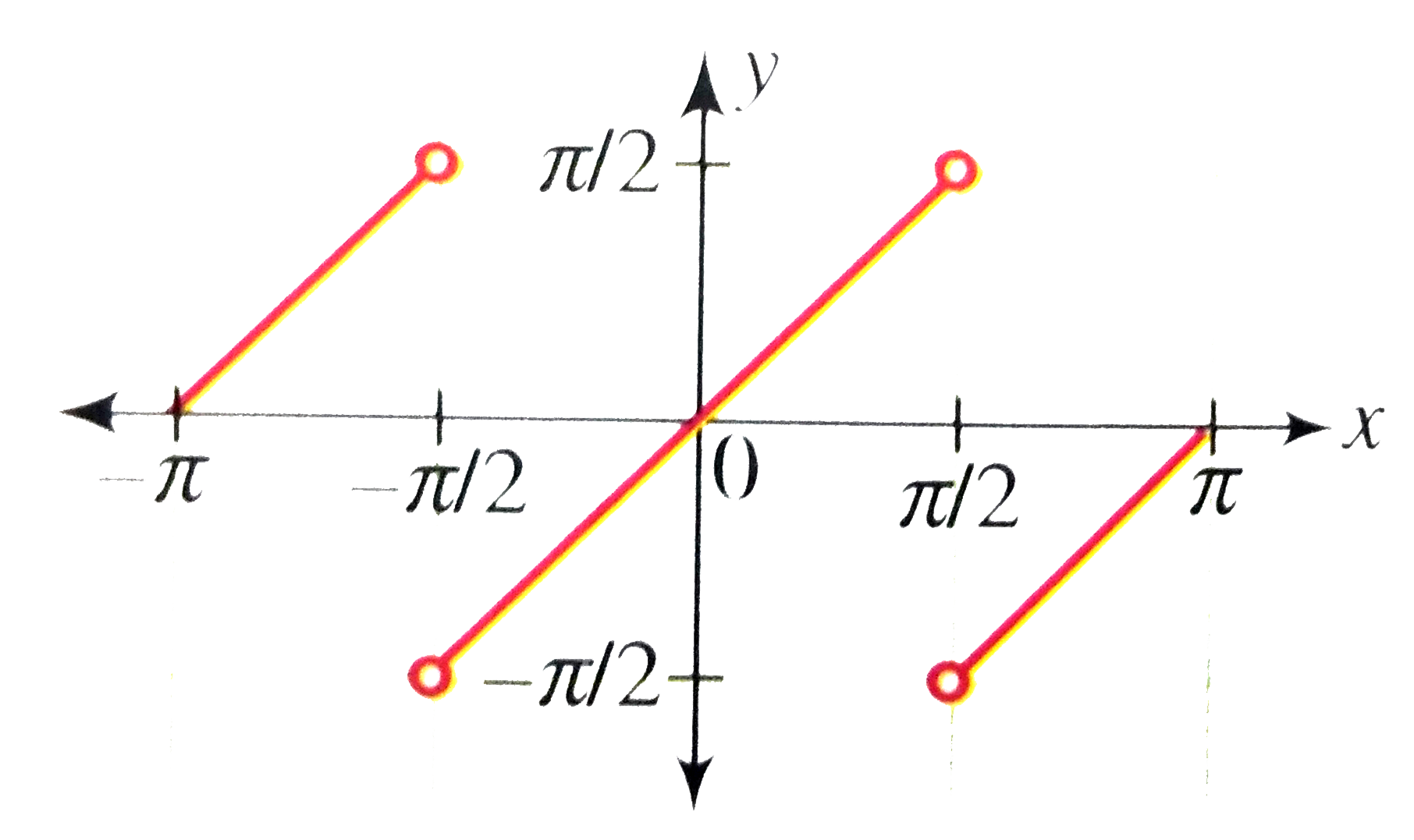
Draw The Graph Of Y Tan 1 2x 1 X 2

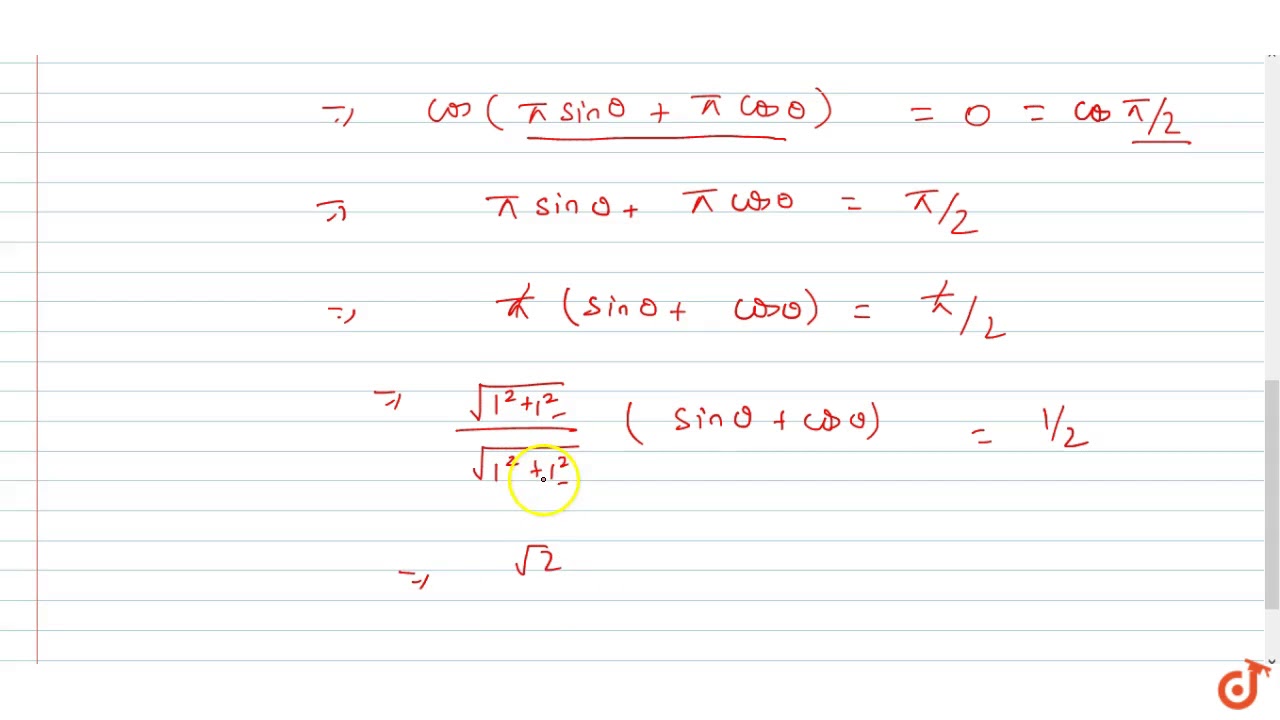
If Tan Pi Cos Theta Cot Pi Sin Theta Then Prove Cos Theta Pi 4 1 2 Sqrt2 Youtube

Consider The Following X Tan 8 Y Sec 8 P 2 Chegg Com

Tan 8 4 3 Where Th Frac P 2 Q 8 Gauthmath

Http Mrsk Ca 12u Practicec1doubleid Pdf

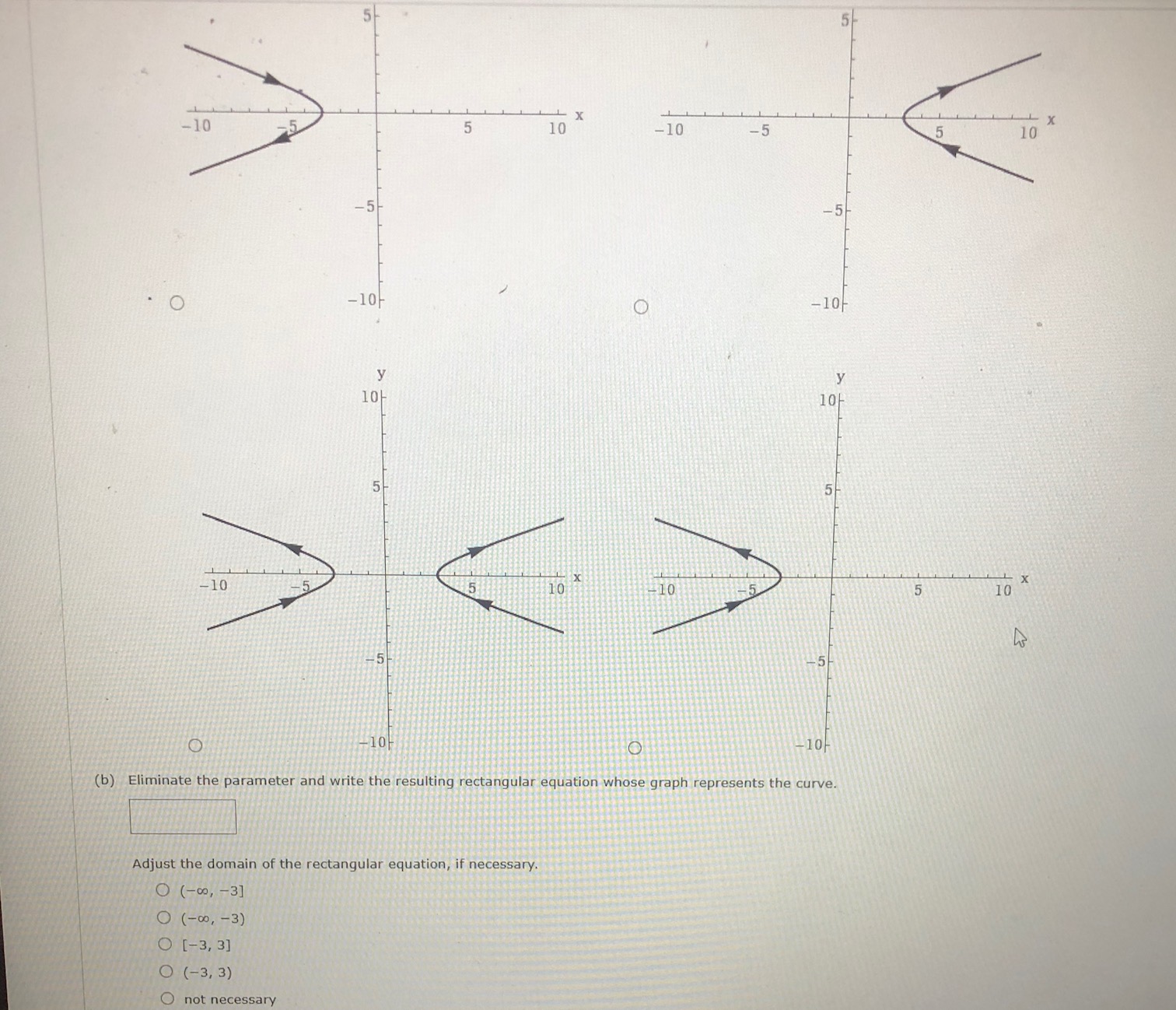
Answered Consider The Following X 3 Sec 8 Bartleby

1

How Do You Find The Exact Value Of Cos Pi 6 Socratic

Cos 2 Theta 1 Sin 2 Theta Tan Pi 4 Theta Brainly In

Find Integral 1 X 2squareroot X 2 9 Dx Let X 3 Chegg Com

18 Find The Cartesian Equation Of The Curve From The Parametric Equations X Tan 2 Theta And Y Sec Theta Where Pi 2 Theta Pi 2 Then Sketch It Width Indication Of

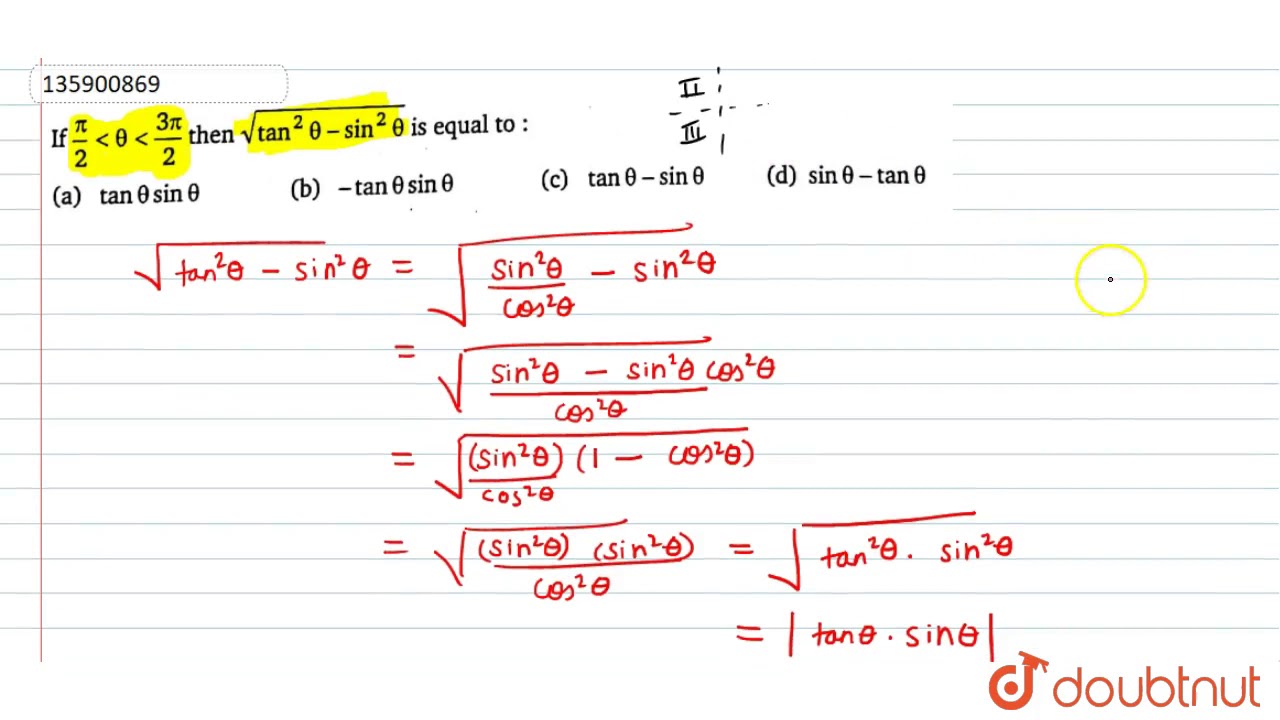
If Pi 2 Lt Theta Lt 3pi 2 Then Sqrt Tan 2 Theta Sin 2 Theta Is Equal To Youtube

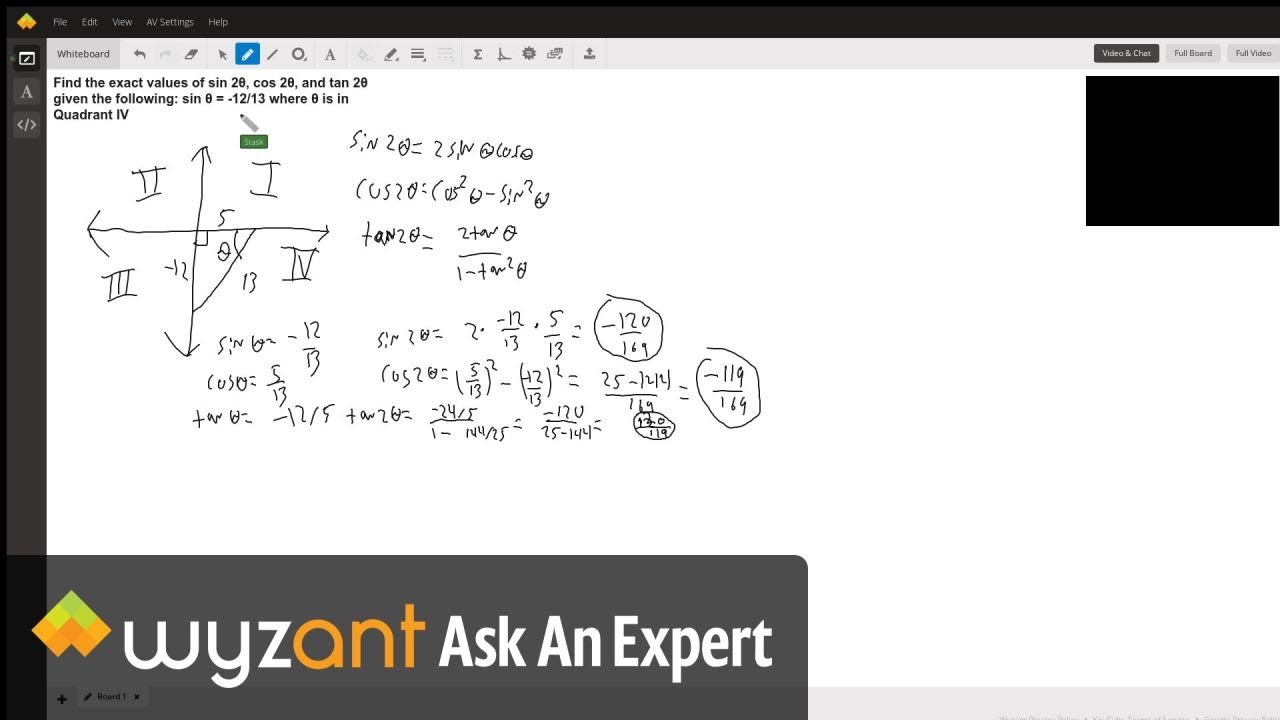
Find The Exact Values Of Sin 28 Cos 28 And Tan 28 Given The Following Sin 8 12 13 Where 8 Is In Quadrant Iv Wyzant Ask An Expert

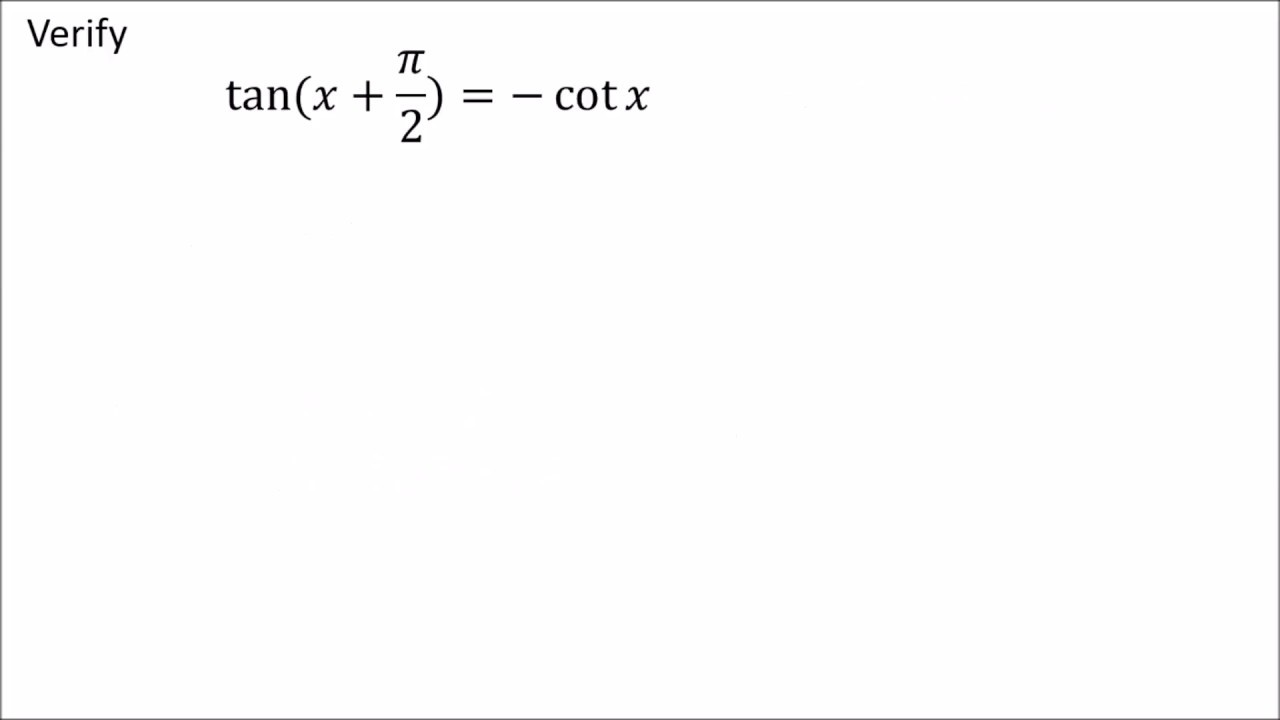
Verify Tan X Pi 2 Cot X Youtube

In Example 1 I Don T Understand How We Got Tan Pi 4 Pi 2 Theta 2 Same Goes For Example 2 Maths Meritnation Com

Sci Pi Prove That Tan P 4 8 Tan P 4 8 2 Sec28 Facebook

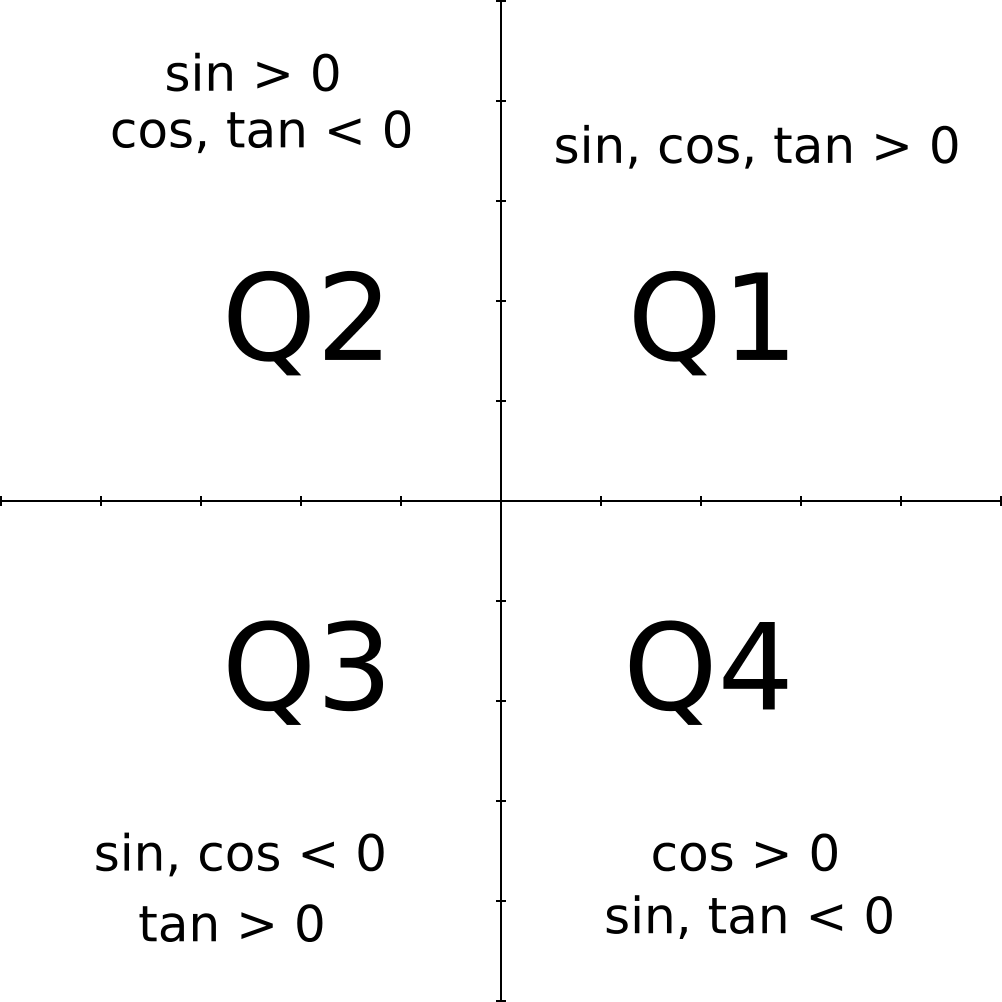
If Cos Theta 5 13 Theta In Quadrant Ii How Do You Find Sin Theta And Tan Theta Socratic

Sinx 1 4 X In Quadrant Ii Find The Value Of Sinx 2

Cofunction Identities In Trigonometry With Proof And Examples Owlcation

Tan P 2 X Cot X 101 Guide For Dummies Youtube

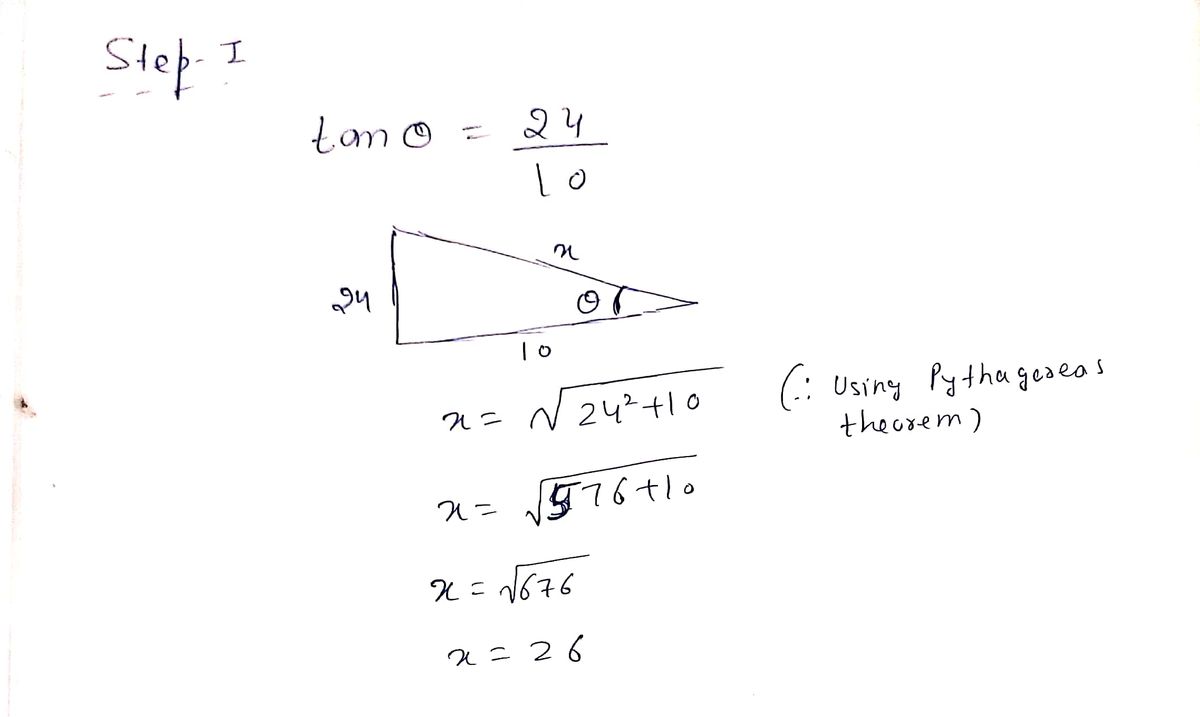
Answered If Tan 8 24 10 0 8 P 2 Bartleby

If Tan Theta Cot Theta 2 Find The Value Of Tan 2 Theta Cot 2 Theta

Cofunction Identities In Trigonometry With Proof And Examples Owlcation

Lim Theta Tends To P 2 Sec Theta Tan Theta Brainly In

4 Prove That 1 2 I Frac Sin 2 P Omega Gauthmath

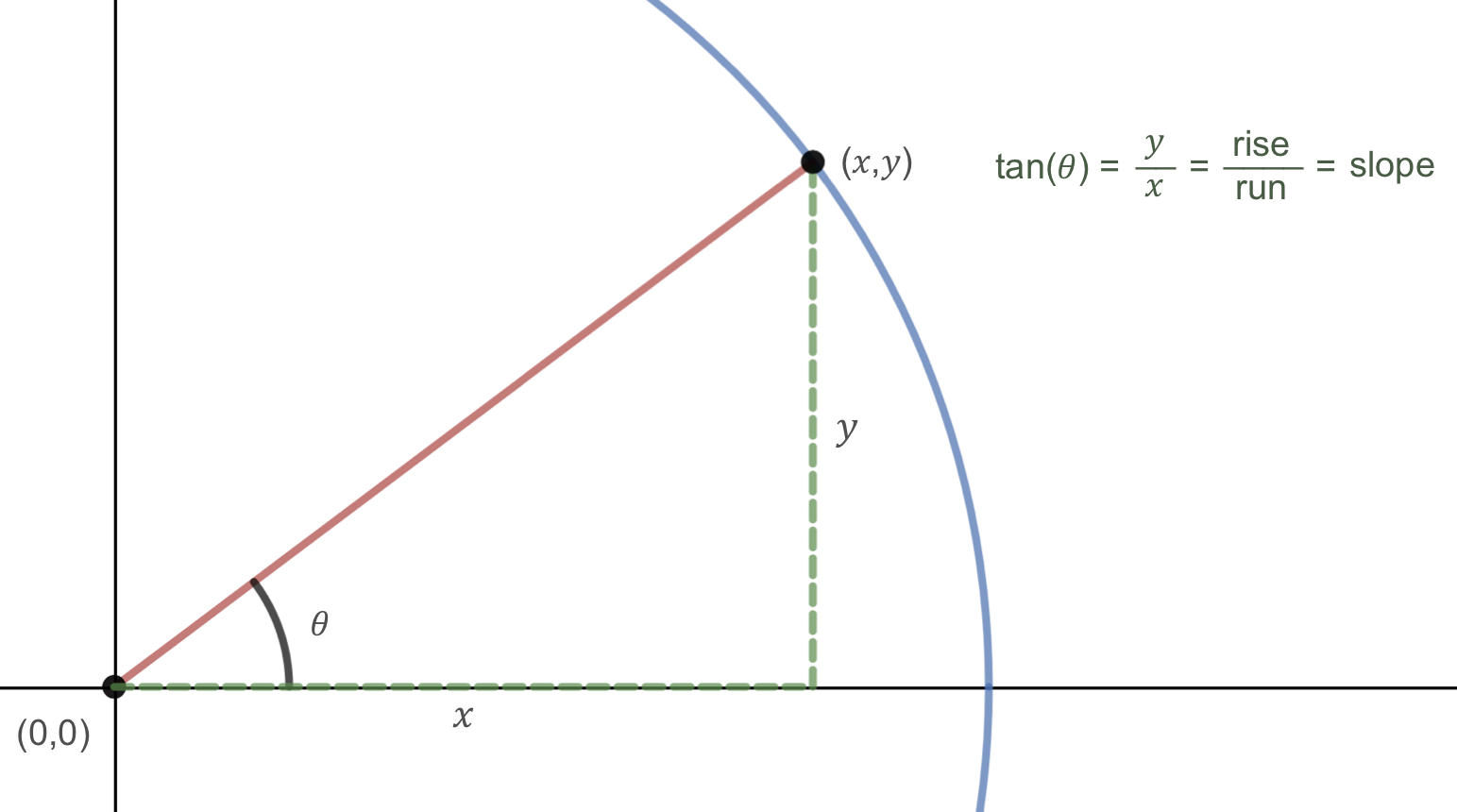
Right Triangle Trigonometry Ppt Download

Ex 3 3 7 Prove Tan Pi 4 X Tan Pi 4 X 1 Tan X 2

The Expression Tan X Pi 2 Cos 3pi 2 X Sin 3 7pi 2 X Cos X Pi 2 Tan 3pi 2 X Simplifies To A Brainly In

If Tan Pi 4 Theta 1 2 Find The Value Of Sin 2 Theta

List Of Trigonometric Identities Wikipedia

Ex 2 2 17 Find Tan 1 Tan 3pi 4 Chapter 2 Class 12 Inverse

Ex 2 1 11 Find Value Tan 1 1 Cos 1 1 2 Sin 1 1 2

Case Fiu Edu Mathstat Resources Math Help Math Help Trigonometry Assets 5 2 Pdf

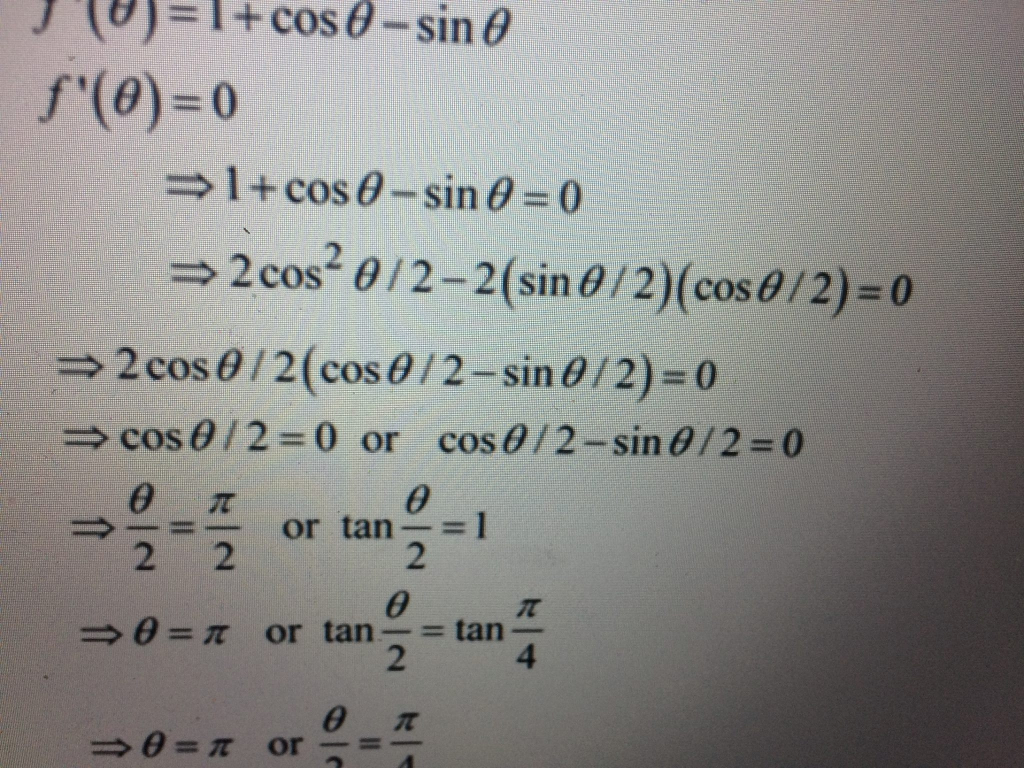
F Theta 0 1 Cos Theta Sin Theta 0 2 Cos 2 Chegg Com

Prove That Sin Pi X Cos Pi2 X Tan 3pi2 X Cot 2pi X Sin 2pi X Cos 2pi X X Sin 3pi2 X N Pi Pi 4 Where N N

Example 3 Find Dx Solution Let X 2 Tan 8 Z 2 Chegg Com

Trigonometric Identities Ppt Download

21 Differentiation And Integration Of Trigonometry Function 9709

Mfg The Tangent Function And Cofunctions

Prove That Tan Pi 4 Theta Tan Pi 4 Theta 2sec2theta

Http Mrsk Ca 12u Practicec1doubleid Pdf

If Tan Pi 2 Theta 2 Sqrt 3 The Value Of Cos Theta Is Youtube

Http Www Mrsfruge Com Uploads 1 2 0 0 Precalculus Chapter 5 Packet Answers Pdf

Basic Trigonometric Functions Trigonometry Socratic

If U Log Tan Pi 4 Teta 2 Then Value Of Is Brainly In

Co Functions Solutions Examples Videos

If X Ln Biggl Tan Bigl Frac Pi 4 Frac Theta 2 Bigr Biggr Then Find Theta Mathematics Stack Exchange

If The Line Y Mx Is Incident To The Point P Theta And Frac Pi 2 Theta Pi Find Sin Theta And Tan Theta Mathematics Stack Exchange

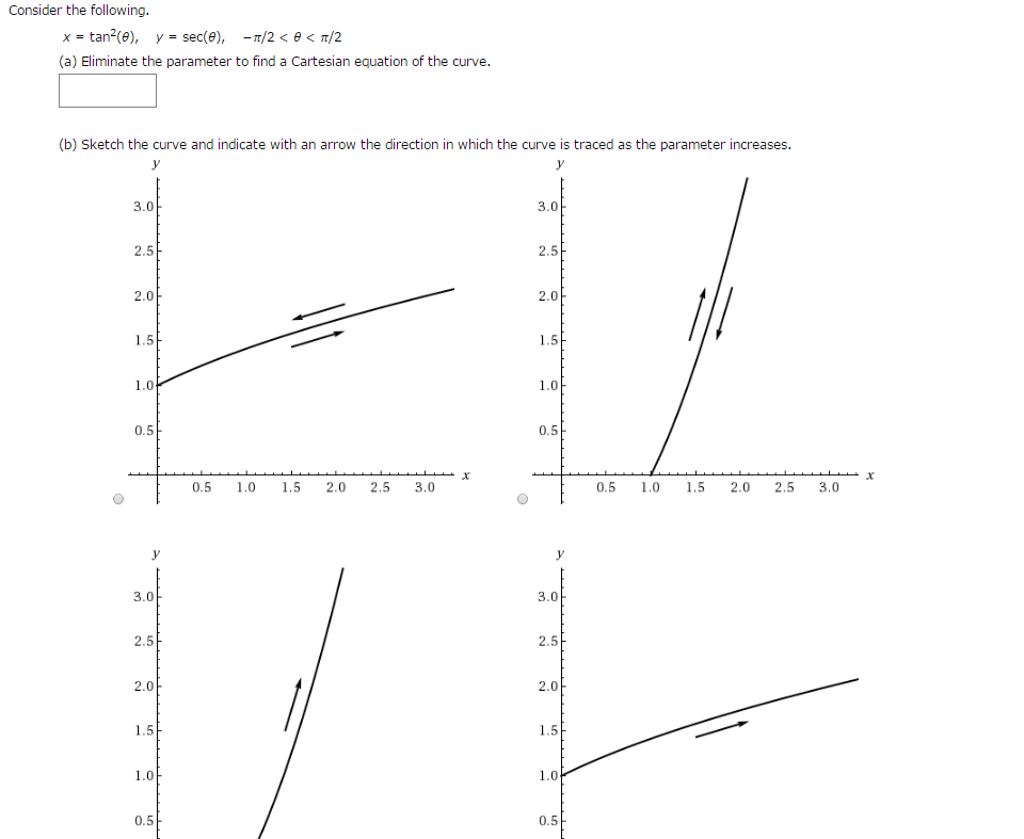
Consider The Following X Tan 2 Theta Y Chegg Com

1

Conf Math Illinois Edu Castelln M117 Lecture10 Math117 Pdf

Grade 12 Math Graphs Of Sinusoidal Functions

Section 2 1 Using Fundamental Identities Ppt Download

Lf U Log Tan Pi 4 Theta 2 Then Tanh U 2

Given That Cos 8 24 25 And Frac 3 P 2 8 Gauthmath

Tan Pi 4 Theta Tan Pi 4 Theta 2tan2theta Youtube

Cos Pi 2

Trigonometric Functions Of Allied Angles Sin Pi Theta Sin Theta Cos Pi Theta Cos Theta Tan Pi Theta Tan Theta Sin 2 Pi Theta Sin Theta Cos 2 Pi Theta Cos Theta Tan 2 Pi Theta Tan Theta Sin Left Frac 3

Prove That Sec Theta Tan Theta Tan Pi 4 Theta 2 Youtube

Solved If U Log Tan Pi 4 Theta 2 Course Hero

Packet 21 Trigonometric Identities Ppt Download

Tan Theta Tan Theta Pi 3 Tan Theta Pi 3 Ktan3theta Find K Askiitians

Tan 180 X Tan Pi X Tan 180 A Tan Pi A Tan 180 Theta Tan Pi Theta Youtube

3

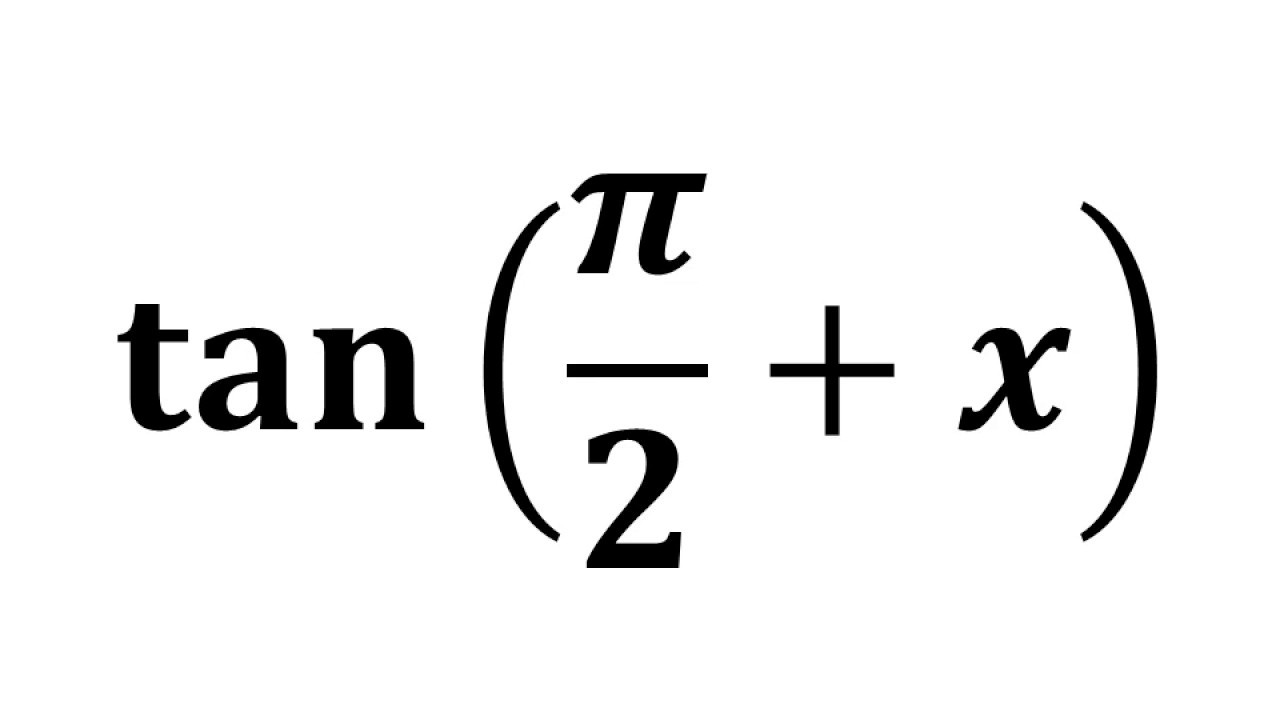
Tan Pi 2 X Tan Pi 2 Theta Youtube

Suppose 3 P 2 8 2 P Tan 8 2 Square Gauthmath

Explicit Function Which Is Tan X Pi 2 X Pi 2 Rotated By For Example 45 Degrees Anticlockwise About Origin Mathematics Stack Exchange

Calculate The Value Of Tan Pi 2 Pi 6 Brainly In

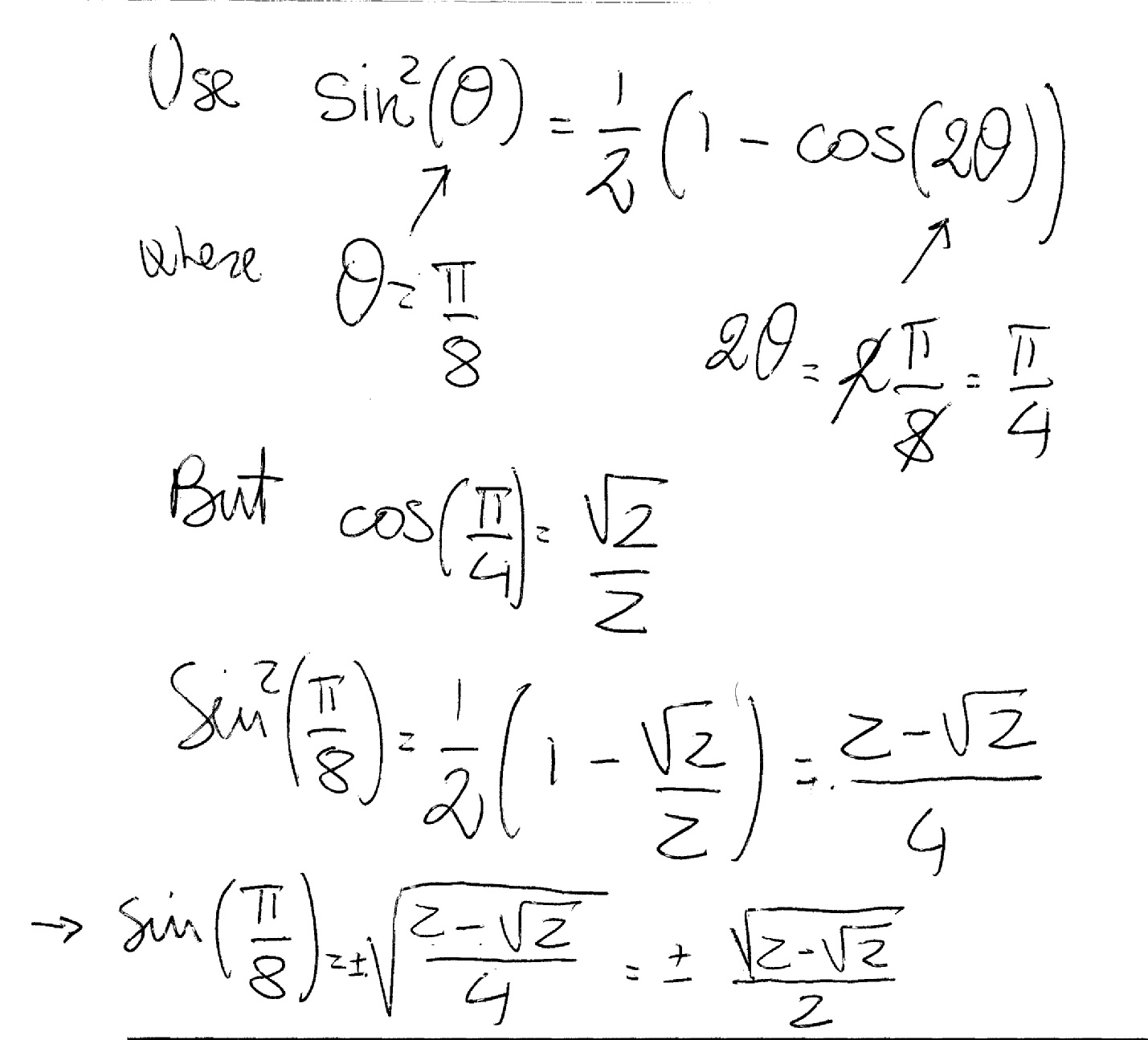
How Do You Use The Half Angle Formula To Simplify Sin 2 Pi 8 Socratic

18 Find The Cartesian Equation Of The Curve From The Parametric Equations X Tan 2 Theta And Y Sec Theta Where Pi 2 Theta Pi 2 Then Sketch It Width Indication Of

If U Logtan Pi4 Theta2 Then Tanh U2

Www Shsu Edu Kws006 Precalculus 4 2 Two Triangles Six Functions Files S 26z 10 3 Pdf

Tan Pi 4 Theta Tan Pi 4 Theta 2sec2theta 1 2si2o1 Tan 0 Tan 4 0 2 Sec Youtube

Example 22 Solve Tan 2x Cot X Pi 3 Teachoo Examples

Solved If U Log Tan Pi 4 Theta 2 Course Hero

Prove That Costheta 1 Sintheta Tan Pi 4 Theta 2

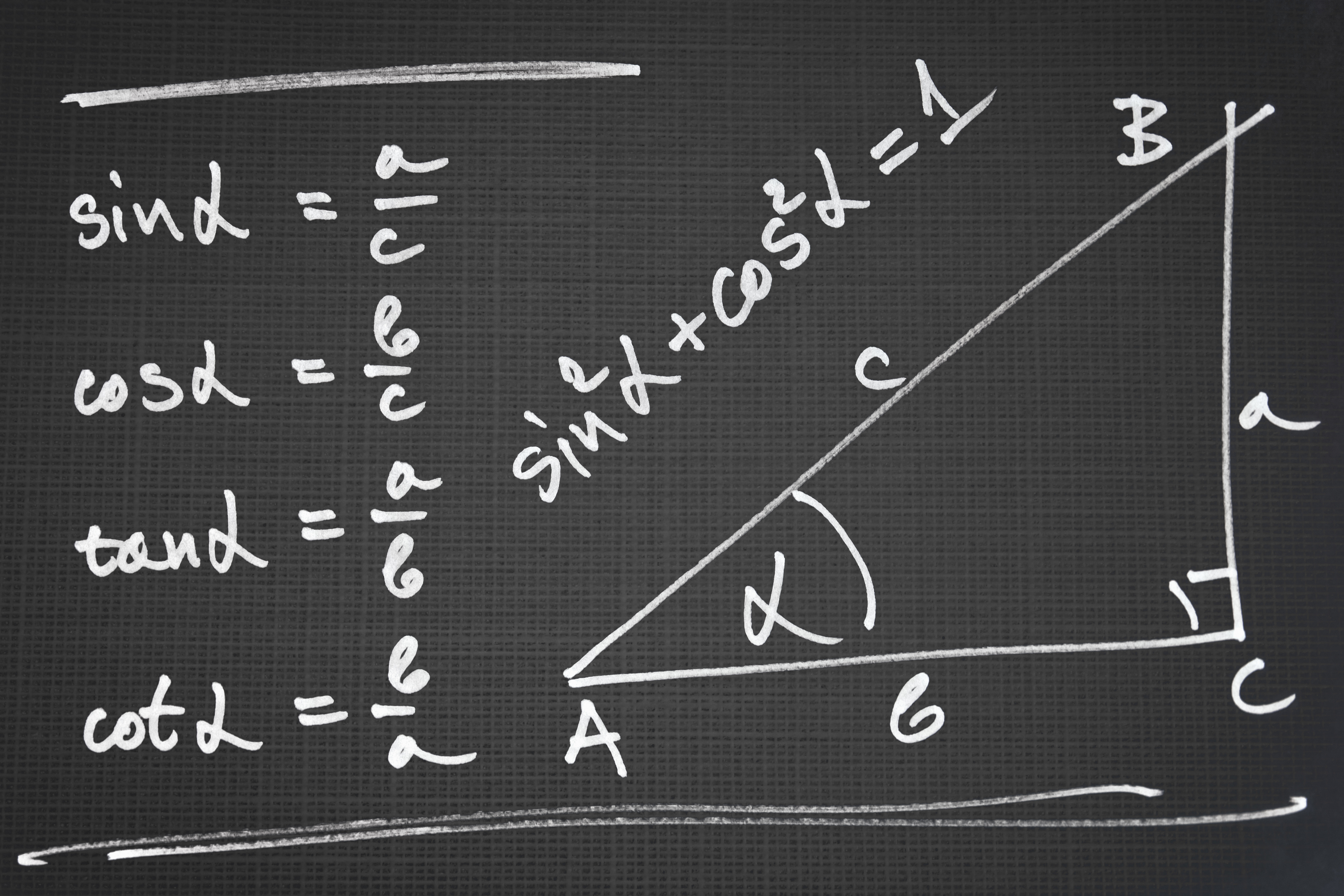
How To Calculate A Cofunction

1

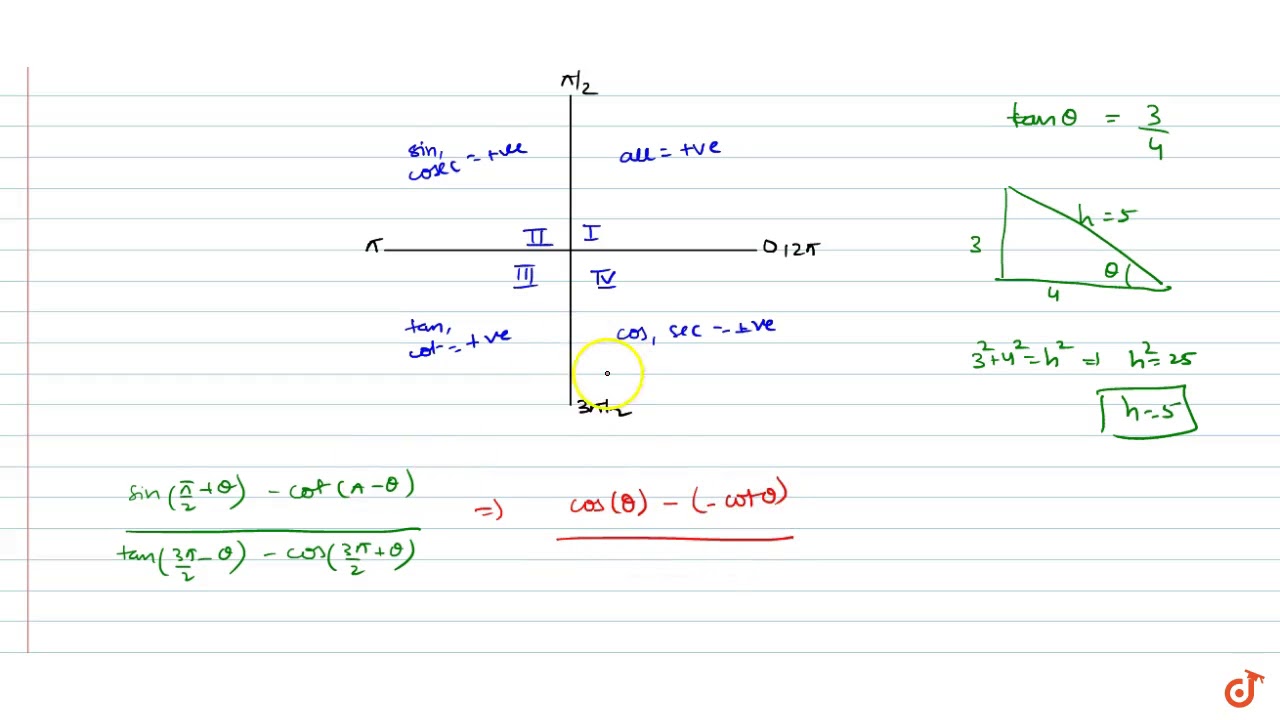
If Tan Theta 3 4 And Theta Is Not In First Quadrant Then Sin Pi 2 Theta Cot Pi Theta Youtube

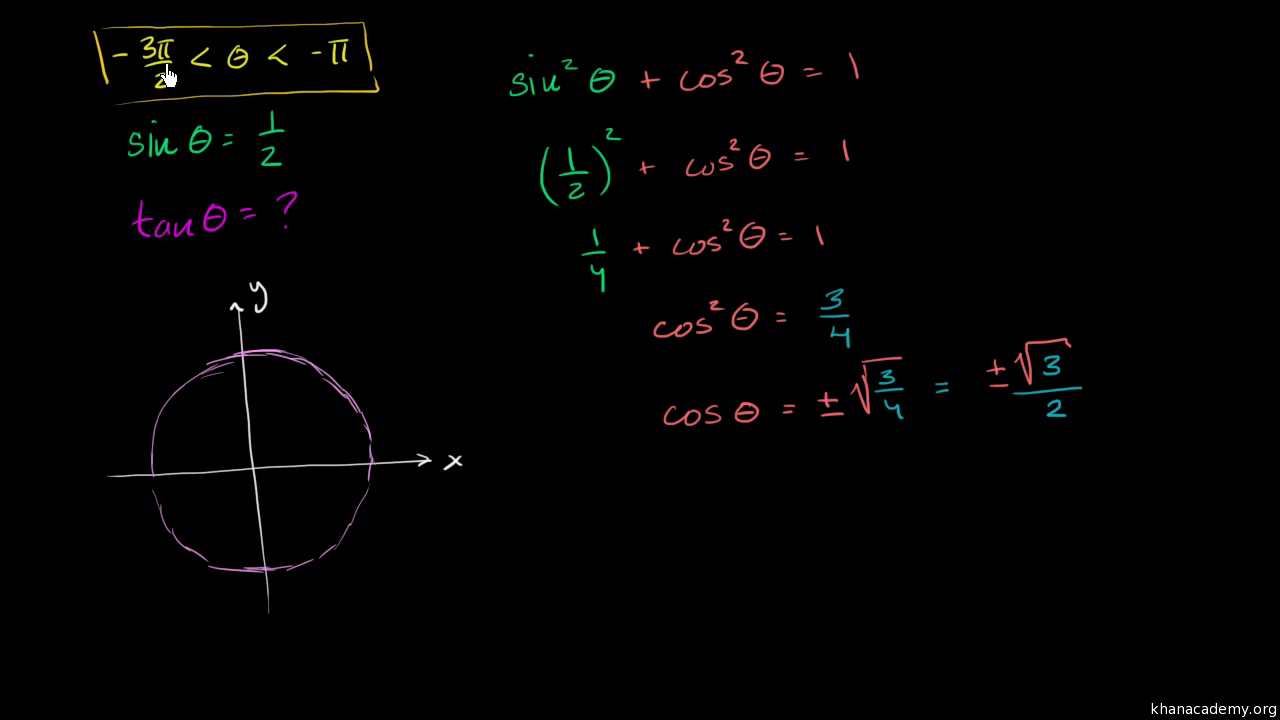
Using The Pythagorean Trig Identity Video Khan Academy

Incoming Term: tan(π/2-θ), tan(θ+π/2)=-1/tan x, tan(π/2+theta), tan(pi/2-theta), tan (π/4 + θ/2), tan pi/2 plus theta, tan 3pi by 2 + theta,